|
Artikel Penelitian oleh : S. Behzadi , Ali A. Alesheikh dan E. Poorazizi PENGANTAR ALGORITMA GENETIKA sebagian besar diyakini bahwa peta raster tidak berguna untuk menemukan jalur terpendek dan umumnya pendekatan vektor lebih umum. Tetapi pendekatan raster apa pun dapat membuka cakrawala baru. Di antara berbagai pendekatan, Algoritma Genetika (GA) dapat berkontribusi secara efektif dalam memecahkan banyak masalah termasuk jalur terpendek di peta raster di mana algoritma tidak efisien. Dalam penelitian ini akan disajikan sebuah novel Genetic Algorithm (GA) untuk menyelesaikan jalur terpendek pada peta raster. Dalam peta raster, setiap jalan ditunjukkan dengan warna tertentu. Beberapa pra-proses dilakukan pada peta raster berdasarkan atribut warna kemudian semua parameter Algoritma Genetikaakan ditentukan. Untuk menemukan yang diusulkan, peta raster sebagai peta jalan perkotaan dipilih. Pada studi kasus, alhasil berhasil menentukan jalur terpendek. Sebagai cabang penting dari grafik dan analisis jaringan, masalah jalur terpendek tradisional memiliki aplikasi yang luas. Artinya, SPP adalah topik penelitian klasik (Cherkassky et al. , 1996; Thorup, 2000; Shi, 1999; Heide dan Vocking, 1999; Goldfarb, 1999). Dengan perkembangan komunikasi, ilmu komputer, sistem lalu lintas dan transportasi dan sebagainya, masalah turunan dari masalah terpendek tradisional menjadi semakin penting dalam kehidupan nyata. Misalnya, dalam jaringan komunikasi, node dan edge memiliki biaya (Li et al., 2006). Ada banyak metode untuk memecahkan jalur terpendek dalam jaringan. Perbedaan antara algoritma ini terkait dengan ketepatan dan kecepatannya. Kesamaan antara sebagian besar algoritma ini adalah bahwa mereka dilakukan pada vektor grafik. Algoritma merupakan salah satu jenis algoritma yang digunakan untuk menyelesaikan banyak masalah. Seperti disebutkan sebelumnya, vektor merupakan bagian penting untuk menemukan jalur terpendek, tetapi peta raster lebih tersedia dan lebih murah daripada peta vektor. Dalam penelitian ini, algoritma genetika baru disajikan untuk memecahkan jalur terpendek pada peta raster. Dalam peta raster, setiap jalan ditunjukkan dengan warna tertentu.Menemukan jalur terpendek diselesaikan dengan menggunakan peta warna dan sedikit informasi tentang jenis jalan berwarna. Genetic Algorithm( GA) adalah teknik optimasi dan pencarian (Horowitch dan Sahani, 1978; Horst dan Pardalos, 1995; Haupt dan Haupt, 2004) berdasarkan prinsip-prinsip genetika dan seleksi alam (Goldberg, 1989; Srinivas dan Patnaik, 1994). ; Bandyopadhyay dan Maulik, 2001; Maulik dan Bandyopadhyay, 2003; Sarkar dkk. , 2003; Saha Misra dkk. , 2001; Mukhopadhyay dkk. , 2000, 2005; Naskar dkk. , 2002). Metode ini dikembangkan oleh John Holland (Holland, 1975) dan rekan-rekannya. Algoritma genetika terbukti secara teoritis dan empiris sebagai teknik pencarian yang kuat (Goldberg, 1989). Algoritma dimulai dengan populasi acak dari solusi kandidat yang dikodekan, yang disebut kromosom. Melalui proses rekombinasi dan operator mutasi, ia mengembangkan populasi menuju solusi yang optimal. Langkah pertama biasanya untuk menemukan setiap solusi kandidat dalam populasi saat ini dan untuk memilih solusi yang paling cocok untuk bertindak sebagai orang tua dari generasi berikutnya dari solusi kandidat. Setelah dipilih untuk reproduksi, tetua digabungkan kembali (menggunakan operator crossover) dan bermutasi (menggunakan operator mutasi) untuk menghasilkan keturunan (Holland, 1975; Whitley, 1994).Tetua yang paling cocok dan keturunannya yang baru membentuk populasi baru, dari proses yang berulang untuk membuat populasi baru (Hosseinali dan Alesheikh, 2008; Godefroid dan Khurshid, 2004). Langkah-langkah dari GA adalah (Ericsson et al. , 2002):
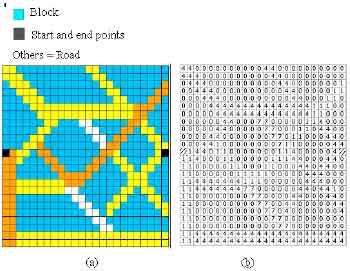
PRA-PENGOLAHAN Pada langkah ini, beberapa proses dilakukan pada peta raster untuk digunakan oleh algoritma genetika. Mula-mula daerah diputar karena titik awal dan titik akhir terletak pada baris yang sama. Dalam peta raster setiap piksel memiliki nilai yang menunjukkan jenis piksel sebagai blok atau jalan. Setiap peta memiliki banyak jenis jalan dan kecepatan kendaraan yang lewat di setiap jenis jalan kira-kira sama. Pada langkah kedua, nilai setiap piksel diubah menjadi nilai integer (Walter et al., 2006) tergantung kecepatan kendaraan di jalan. Jalan di mana kendaraan dapat bergerak lebih cepat diwakili oleh nilai yang lebih kecil. Misalnya pada peta raster yang memiliki dua jenis jalan raya yaitu jalan raya dan jalan raya nilai jalan raya dianggap 1 dan nilai jalan raya dilambangkan dengan 4. Hal ini menunjukkan bahwa kecepatan di jalan raya empat kali lebih cepat daripada kecepatan di jalan raya. .
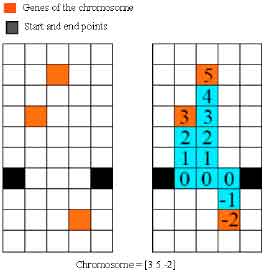
Dalam hal ini nilai balok bangunan dianggap 0`. Proses ini ditunjukkan pada Gambar. 1 . PENERAPAN Setiap piksel pada peta memiliki nilai yang diperoleh dari tahap pra-pemrosesan. Panjang individu dipilih sama dengan jumlah piksel horizontal yang terletak di antara titik awal dan akhir. Misalnya panjang individu untuk peta sampel yang ditunjukkan pada Gambar 1 adalah 22. Pengkodean: Dalam masalah ini, pengkodean permutasi digunakan. Dalam pengkodean permutasi, setiap gen dianggap sebagai bilangan bulat dan bilangan tersebut dianggap sebagai kromosom (Ling dan Meng, 2006). Nilai setiap gen sesuai dengan jumlah piksel yang berada di antara titik yang dipilih dan garis yang terhubung antara titik awal dan titik akhir. Misalnya [3 5 -2] sebagai pengkodean yang sesuai dengan kromosom pada Gambar. 2 . Pra-pemrosesan dan metode pengkodean ini mampu menghasilkan semua individu yang layak melalui operasi genetik seperti persilangan atau mutasi. Populasi awal: Dalam masalah ini, populasi awal dibangkitkan secara acak (Duan dan Yu, 2003). Ini berarti bahwa gen dari setiap kromosom yang ditentukan dengan memilih nomor acak antara L min dan L max , di mana L min dan L max adalah jumlah piksel yang ada di bawah dan di atas garis penghubung antara titik awal dan titik akhir masing-masing dalam satu titik . kolom Jumlah kolom sama dengan posisi gen yang dipilih.
Fungsi kebugaran: Fungsi kebugaran dalam penelitian ini didefinisikan sebagai:
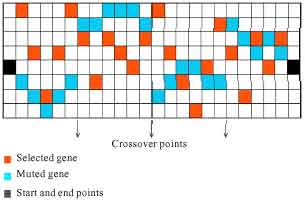
Penskalaan kebugaran: Penskalaan kebugaran mengonversi skor kebugaran mentah yang dikembalikan oleh fungsi kebugaran ke nilai dalam rentang yang sesuai untuk orang tua terpilih untuk menghasilkan keturunan. Dalam penelitian ini, penskalaan proporsional digunakan untuk membuat nilai skala dari suatu individu sebanding dengan skor kebugaran mentahnya. Operator genetika: Bagian terpenting dari algoritma genetika adalah operator genetika: crossover dan mutasi. Efisiensi dan kecepatan pemecahan masalah tergantung pada definisi parameter ini. Pada permasalahan ini, operator mutasi dan crossover tidak dilakukan secara bersamaan. Mula-mula operator mutasi dilakukan pada peta untuk membuat ruas jalan yang sebenarnya kemudian jalan yang lengkap dibuat dengan menggunakan operator crossover. Operator mutasi: Pada awal, garis yang terhubung antara titik dan titik akhir dibagian m bagian di mana m adalah bilangan acak yang lebih dari piksel antara titik awal dan titik akhir. Untuk setiap bagian, dari gen acak pertama hingga gen terakhir, setiap piksel bermutasi secara berurutan menurut piksel lain yang terletak di kolom yang sama dan jarak antara piksel yang saat ini mendapatkan mutasi dan piksel yang sebelumnya bermutasi harus kurang dari dua piksel. Nilai gen bermutasi yang dihitung pada langkah pra-pemrosesan tidak boleh 0`. Jenis ini ditunjukkan pada Gambar. 3 . Operator crossover: Dalam penelitian ini, operator crossover n-titik digunakan untuk membuat jalan lengkap sebagai solusi untuk masalah di mana n adalah bilangan acak antara 1 sampai m?1 (m adalah bilangan yang didefinisikan dalam operator mutasi). Misalnya jika n sama dengan 2 maka digunakan crossover 2 titik.
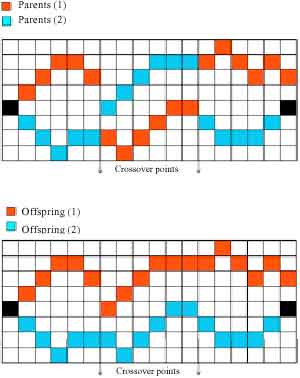
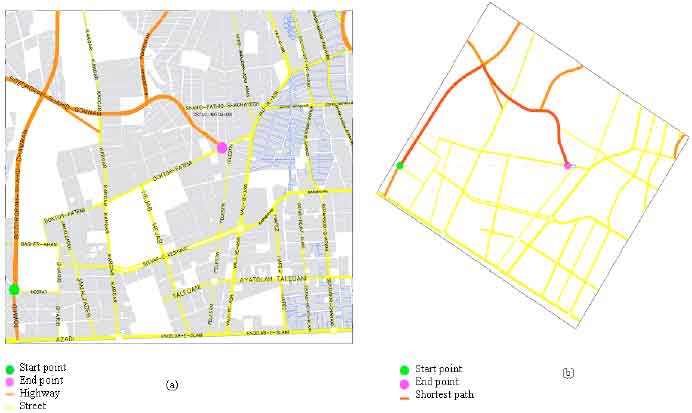
Pada persilangan dua titik, dipilih 2 titik, gen dari awal kromosom ke titik persilangan pertama disalin dari induk pertama, dari titik persilangan pertama ke kedua disalin dari induk kedua dan sisa disalin dari orang tua pertama (Davies dan Lingras, 2003; Yen et al . , 2007). Crossover dua titik ditunjukkan pada Gambar. 4 . HASIL DAN DISKUSI Untuk mengilustrasikan hasil metode yang diusulkan, peta raster berwarna sebenarnya dari Teheran, ibu kota Iran. Tujuannya adalah untuk menemukan jalan dengan waktu minimum. Hasil percobaan ditunjukkan pada Gambar 5 .
Algoritma genetika adalah algoritma yang efisien yang digunakan untuk memecahkan banyak masalah. Algoritma ini adalah algoritma umum dan setiap masalah dapat diselesaikan dengan algoritma ini. Menemukan jalur terbaik adalah jenis masalah yang membutuhkan vektor grafik untuk memecahkannya. Banyak yang dirancang untuk masalah ini dan platform paling dasar dari mereka adalah grafik vektor. Dalam makalah ini, seperti yang disebutkan di atas, ada beberapa batasan dalam menggunakan peta vektor. Oleh karena itu peta raster digunakan untuk masalah ini. Menggunakan GA, dicoba untuk menemukan jalur terpendek pada peta raster.Pada awalnya beberapa pra-pemrosesan dilakukan pada peta termasuk mengubah nilai semua piksel di peta berdasarkan informasi tentang warna jalan dan memutar area berdasarkan titik awal dan akhir. Pada penelitian ini hanya digunakan peta raster. Kita dapat menggunakan peta raster dan vektor secara bersamaan. Dalam hal ini, operator baru harus didefinisikan berdasarkan masalah baru atau peta vektor dapat diubah menjadi peta raster. Dalam hal ini, kami hanya memiliki peta raster kemudian jalur terpendek diselesaikan dengan metode yang diusulkan.
|